FFT Spectra

O programu

Program fft-spectra umožňuje v reálném čase sledovat frekvenční rozklad zvukového záznamu nebo mikrofonového vstupu. K čemu je to dobré? S pomocí programu fft-spectra může člověk například

- ověřit, jestli zpívá/píská falešně
- snadno a rychle naladit kytaru/housle
- uspokojit vrozenou zvídavost a dozvědět se něco z fyziky hudby ;-)

Proč ten divný název? FFT je zkratka z anglického "Fast Fourier Transform", rychlá Fourierova transformace. Fourierova transformace je důležitý matematický nástroj se závratně mnoha praktickými aplikacemi. Například zní-li ve zvukovém záznamu mnoho různých tónů současně, lze s pomocí Fourierovy transformace zjistit frekvence všech přítomných tónů.

Ke stažení

Program běží na Linuxu a je volně ke stažení pod licencí GPL. Projekt běží na stránkách SourceForge.

Kontakt

Preferovaný způsob kontaktu je prostřednictvím mail-konference v angličtině. Případně je možné poslat e-mail přímo mně: Petr Daněček,

Ukázky

Didgeridoo

Celý program vznikl díky Didgeridoo. Je to prastarý hudební nástroj s příjemným zvukem (údajně známý už 40000 let) a v moderní době nalezl nečekané uplatnění v hodinách fyziky, konkrétně při výkladu o akustice a stojatém vlnění. V dalším textu budu předpokládat že víte:

Co je to zvuk: ... opakované změny tlaku vzduchu, periodické v čase i prostoru
Co je to stojaté vlnění: ... vlna se v čase neposouvá, oblast s maximální i nulovou výchylkou zůstávají na jednom místě
Co je to frekvence: ... počet opakování (čehokoliv) za jednu vteřinu
A rovněž je užitečné vědět, jak souvisí délka vlny s frekvencí: ... při dané rychlosti zvuku projde daným místem za jednotku času více vln s kratší délkou, tj. frekvence je vyšší. Dlouhých vln projde méně, tj. frekvence je nižší.

(Klikni na obrázek pro větší verzi.)

Z fyzikálního hlediska je Didgeridoo válcová dutina otevřená na obou koncích. Z jedné strany se do ní fouká a přitom se vibruje rty. Asi tak jako kdybychom chtěli napodobit zvuk auta bez použití hlasivek. Uvnitř dutiny vzniká stojaté vlnění, které musí na obou koncích splňovat následující okrajové podmínky:
Na otevřeném konci trubice, kudy vzduch vychází ven, tvoří okolní prostor obrovský rezervoár konstantního tlaku - stojaté vlnění zde má proto uzlový bod. Na druhém konci, kterým se fouká dovnitř, jsou změny tlaku největší a stojaté vlnění zde má kmitnu.

Na obrázku vpravo je situace zachycena schematicky: Vodorovná osa znázorňuje polohu na trubici a na svislé ose je vynesený tlak v daném místě jako maximální odchylka od průměrného tlaku. Černá vodorovná čára znázorňuje nulovou výchylku. Levý puntík odpovídá konci, do kterého foukáme. Maximální možná odchylka od průměrného tlaku (neboli amplituda vlnění) je zde největší. Puntík napravo odpovídá volnému konci - amplituda je zde prakticky nulová.

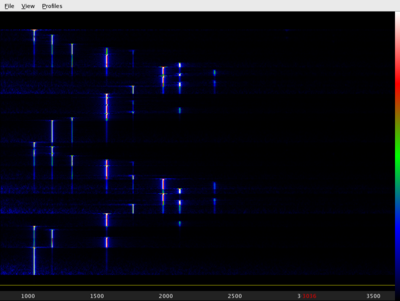
Okrajová podmínka požadující na jednom konci kmitnu a na druhém konci uzlový bod potom vymezuje, jaké frekvence (tj. jak dlouhé vlny) se mohou v této dutině realizovat a naopak které budou zakázané. Takže například červená křivka znázorňuje nejnižší (základní) frekvenci přítomnou ve zvuku didgeridoo. (Odpovídá frekvenci 70Hz na spodním obrázku.) Kdybychom tuto vlnu dvakrát "stlačili" jako harmoniku, dostali bychom na obou koncích kmitny - frekvence odpovídající této vlně jsou zakázané, protože podmínka kmitna-uzel není splněná. A skutečně: tato (nezakreslená) křivka s 2x větší frekvencí odpovídá ve skutečném spektru takřka neznatelnému vrcholku na 140Hz. Když však vlnu stlačíme ještě o trochu víc, dostaneme zelenou křivku, která okrajové podmínky splňuje. Na obrázku dole odpovídá frekvenci 210Hz...

Zajímalo mě: Platí toto pravidlo lichých harmonických frekvencí vždy? Chtěl jsem sledovat spektrum v reálném čase a pozorovat jak se mění se zvuky, které didgeridoo vydává. Vyzkoušejte sami, co didgeridoo dokáže!

Odkazy

O stojatém vlnění a pohybu vzduchu ve válcové dutině. (Anglické stránky s velice ilustrativními obrázky a řadou dalších hudebních nástrojů.)
Podrobněji o fyzice didgeridoo.
Jemný úvod do fyziky hudby.

(Klikni na obrázek pro větší verzi.)

Zvonkohra

Andělský zvuk zvonkohry (neplést s xylofonem) atd...